ČSN ISO 2041 - Vibrace, rázy a monitorování stavu – Slovník
| Stáhnout normu: | ČSN ISO 2041 (Zobrazit podrobnosti) |
| Datum vydání/vložení: | 2020-04-01 |
| Zdroj: | https://www.iso.org/obp/ui#iso:std:iso:2041:ed-4:v1:en |
| Třidící znak: | 011400 |
| Obor: | Mechanika |
| ICS: |
|
| Stav: | Platná |
3.1.58 dynamická tuhost
(dynamic stiffness) dynamická konstanta pružiny (dynamic elastic constant; dynamic spring constant) komplexní poměr síly měřené v určitém bodě mechanické soustavy k výchylce měřené ve stejném nebo v jiném bodě soustavy POZNÁMKA 1 k heslu Dynamická tuhost může být závislá na napětí (amplitudě a frekvenci), rychlosti přetvoření, teplotě nebo na jiných podmínkách. POZNÁMKA 2 k heslu Komplexní dynamická tuhost se rovná kde je c koeficient lineárního (viskózního) tlumení; e základ přirozených logaritmů; F0 amplituda síly; i k konstanta pružiny; m hmotnost; t čas; x výchylka; x0 amplituda výchylky;
Legenda X frekvence v hertzech (Hz) Y1 fázový úhel ve stupních Y2 velikost pohyblivosti v decibelech (dB), [ref. 1 m/(N·s)] a klesající úsečky odpovídají hmotnosti b stoupající úsečky odpovídají tuhosti Obrázek 1 – Diagram pohyblivosti 
Legenda X frekvence v hertzech (Hz) Y akcelerance v decibelech (dB), [ref. 1 m/(N·s2)] a stoupající úsečky odpovídají tuhosti b vodorovné úsečky odpovídají hmotnosti Obrázek 2 – Diagram velikosti akcelerance odpovídající diagramu pohyblivosti na obrázku 1 
Legenda X frekvence v hertzech (Hz) Y dynamická poddajnost v decibelech (dB), [ref. 1 m/N] a vodorovné úsečky odpovídají tuhosti b klesající úsečky odpovídají hmotnosti Obrázek 3 – Diagram velikosti dynamické poddajnosti odpovídající diagramu pohyblivosti na obrázku 1
3.1.58 dynamic stiffness
dynamic elastic constant dynamic spring constant complex ratio of the force, taken at a point in a mechanical system, to the displacement, taken at the same or another point in the system Note 1 to entry: The dynamic stiffness may be dependent upon the strain (amplitude and frequency), strain-rate, temperature or other conditions. Note 2 to entry: The complex dynamic stiffness, k*, of a linear translational single-degree-of-freedom system characterized by the equation where F = F0 eiωt and is equal to wherec
is the linear (viscous) damping coefficient;
e
is the base of natural logarithms;
F0
is the force amplitude;
i
; k
is the elastic (spring) constant;
m
is the mass;
t
is the time;
x
is the displacement;
x0
is the displacement amplitude;
ζ
is the damping ratio;
ω
is the angular frequency;
EMBED Equation.DSMT4
is the natural angular frequency.
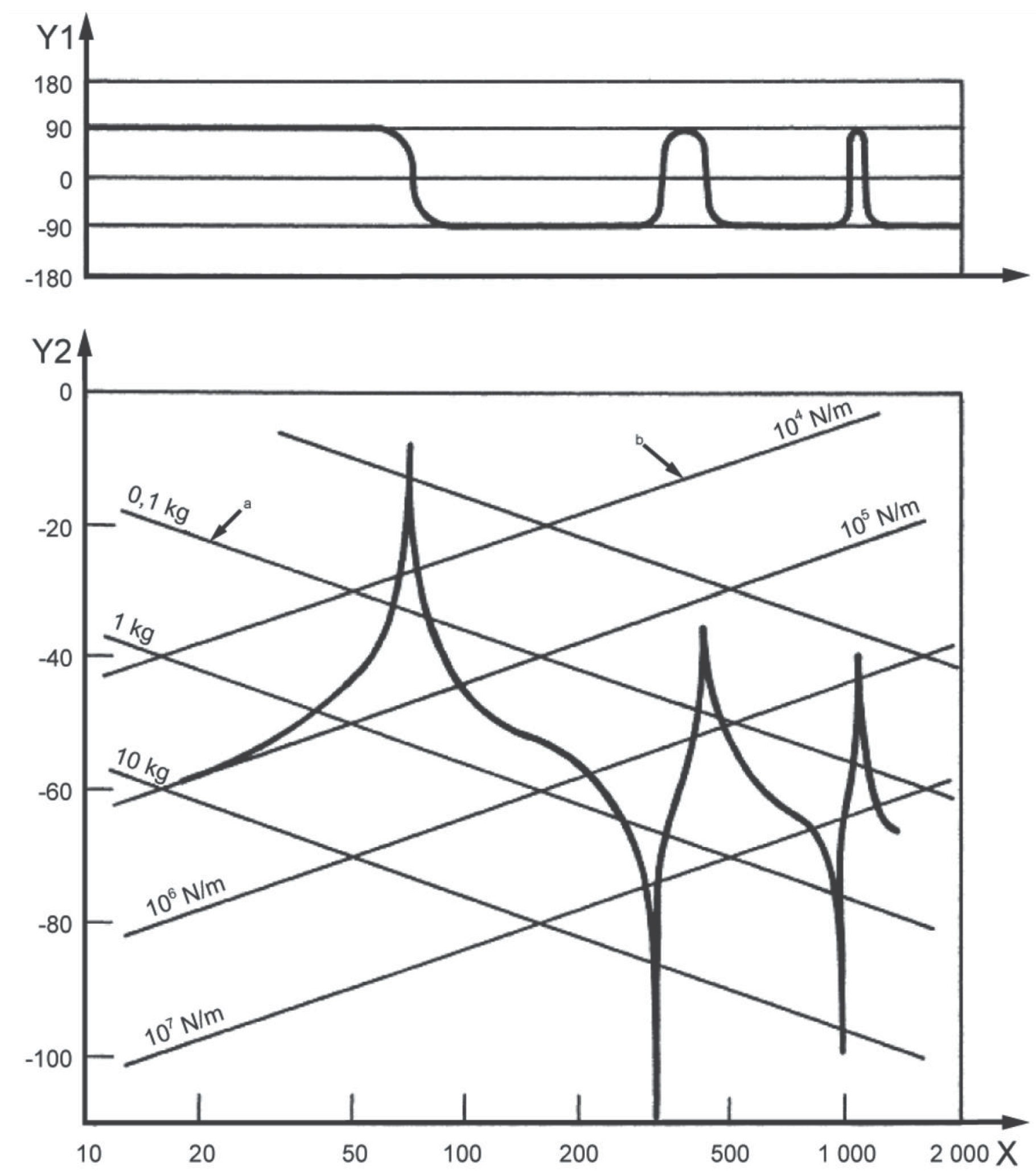Key X
frequency, in hertz (Hz)
Y1
phase angle, in degrees
Y2
mobility magnitude, in decibels (dB), [ref. 1 m/(N⋅s)]
a
Downwards sloping lines are used for mass.
b
Upwards sloping lines are used for stiffness.
Figure 10\IF >= 1 "A." — Mobility plot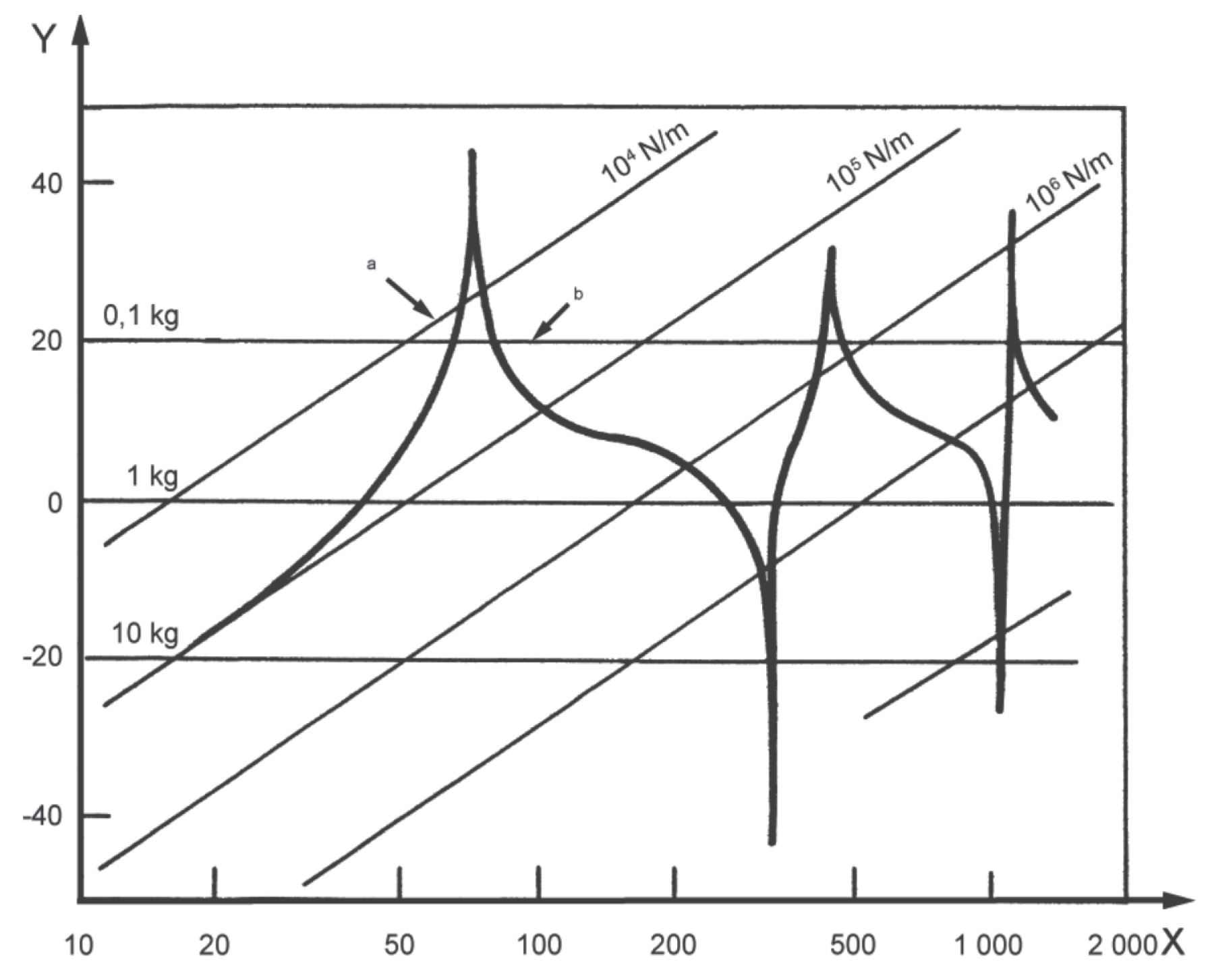
Key X
frequency, in hertz (Hz)
Y
accelerance, in decibels (dB), [ref. 1 m/(N⋅s2)]
a
Upwards sloping lines represent stiffness.
b
Horizontal lines represent mass.
Figure 20\IF >= 1 "A." — Accelerance magnitude plot corresponding to the mobility graph plotted in Figure 1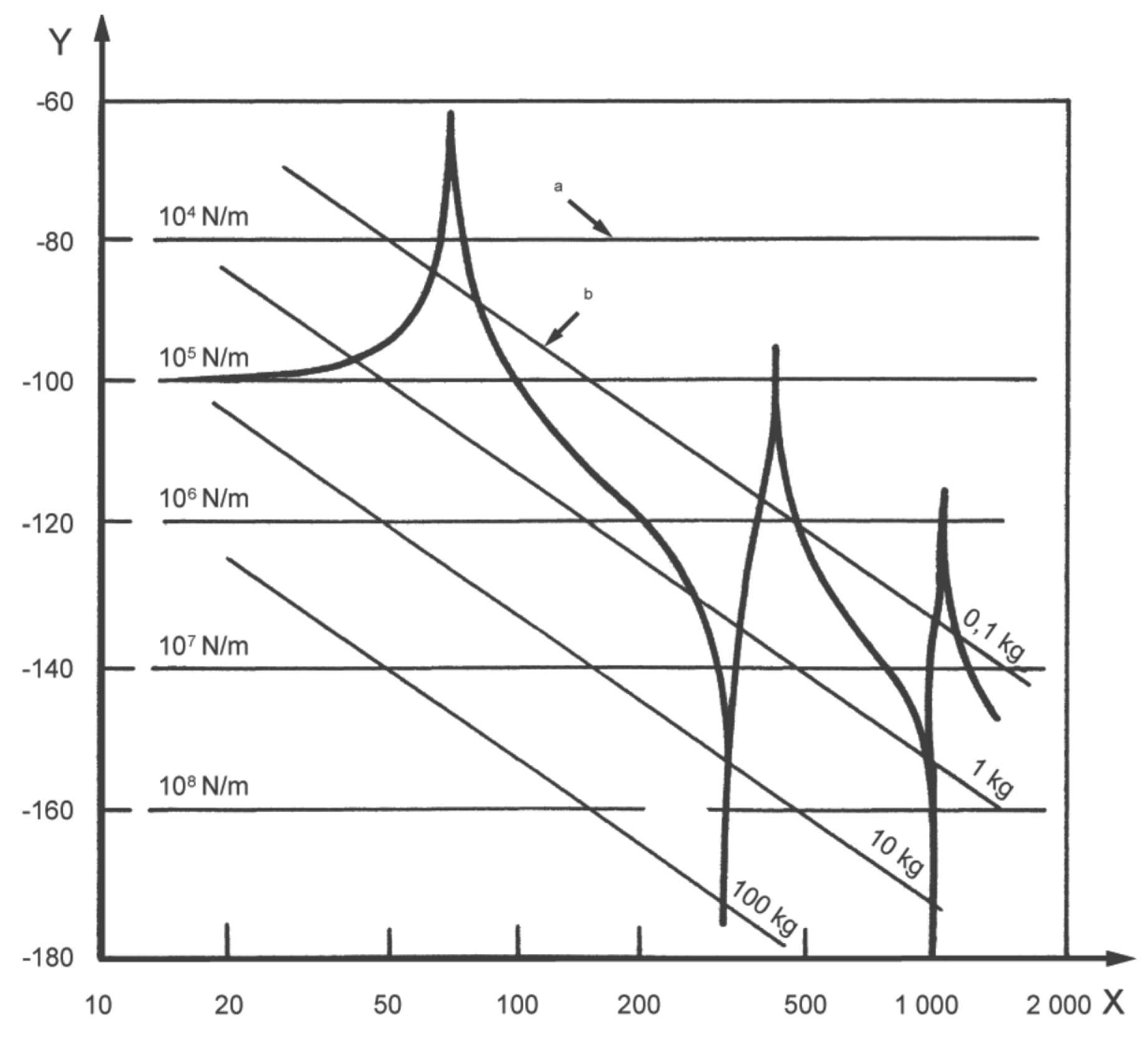
Key X
frequency, in hertz (Hz)
Y
dynamic compliance, in decibels (dB), [ref. 1 m/N]
a
Horizontal lines represent stiffness.
b
Downwards sloping lines represent mass.
Figure 30\IF >= 1 "A." — Dynamic compliance magnitude plot corresponding to the mobility graph plotted in Figure 1